1. Linked List:
vLinear collection of nodes
vDoesn’t store its nodes in consecutive memory locations
vCan be accessed only in a sequential manner
there are types of linked list:
1. Single Linked List
In a singly linked list, each node stores a reference to an object that is an element of the sequence, as well as a reference to the next node of the list. It does not store any pointer or reference to the previous node.
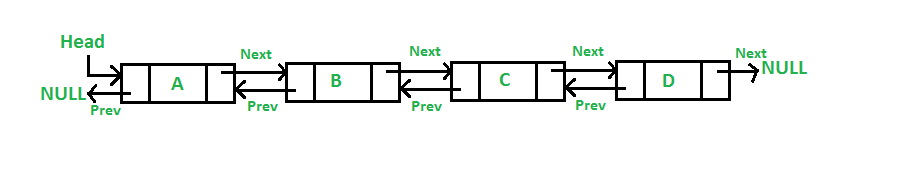
 2. Double Linked List
2. Double Linked List
2. Stack

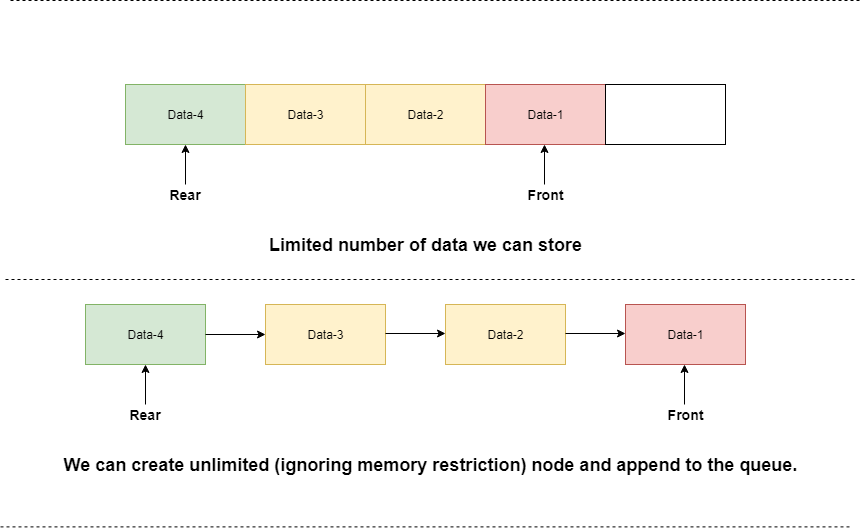
3. Queue
4. Hashing
5. Hash Table
6. Tree and Binary Tree
Tree Concept
•Node at the top is called as root.
7. Binary Search Tree
•Binary Search Tree (BST) is one such data structures that supports faster searching, rapid sorting, and easy insertion and deletion.
In a singly linked list, each node stores a reference to an object that is an element of the sequence, as well as a reference to the next node of the list. It does not store any pointer or reference to the previous node.
To store a single linked list, only the reference or pointer to the first node in that list must be stored. The last node in a single linked list points to nothing.

A Double Linked List (DLL) contains an extra pointer, typically called previous pointer, together with next pointer and data which are there in single linked list.

• Stack is a collection data
structure which has two fundamental operation: push
and pop.
• The data are stored in Last
In First Out (LIFO) way.
• Stack can be implemented using
array or linked
list *.
• Implementing stack using array is much “easier” than using linked list.
• One example of implementing stack is conversion from infix to prefix and postfix.
• Queue is a collection data
structure which has two fundamental operation: push
and pop (similar to stack).
• The data are stored in First
In First Out (FIFO) way,
this is the main difference between stack and queue.

- Hashing is a technique used for storing and retrieving keys in a rapid manner.
- Hashing can also be defined as a concept of distributing keys in an array called a hash table using a predetermined function called hash function.
- Hash table is a table (array) where we store the original string. Index of the table is the hashed key while the value is the original string.
- The size of hash table is usually several orders of magnitude lower than the total number of possible string, so several string might have a same hashed-key. example of hash fuction:
There are many ways to hash a string into a key for constructing hash functions:
- Mid-Square Square the string/identifier and then using an appropriate number of bits from the middle of the square to obtain the hash-key.
Steps:1. Square the value of the key. (k2)2. Extract the middle r bits of the result obtained in Step 1.
Function : h(k) = s
k = key
s = the hash key obtained by selecting r bits from k2
2. Division
Divide the string/identifier by using the modulus operator.
It’s the most simple method of hashing an integer x.
Function: h(z) = z mod M
z = key
M = the value using to divide the key, usually using a prime number, the table size or the size of memory used.
3. Folding
The Folding method works in two steps :
a. Divide the key value into a number of parts where each part has the same number of digits except the last part which may have lesser digits than the other parts.
b. Add the individual parts. That is obtain the sum of part1 + part2 + ... + part n. The hash value produced by ignoring the last carry, if any.
4. Digit Extraction
A predefined digit of the given number is considered as the hash address.
5. Rotating Hash
Use any hash method (such as division or mid-square method)
After getting the hash code/address from the hash method, do rotation.
Rotation is performed by shifting the digits to get a new hash address.
Collision
What happened if we want to store these strings using the previous hash function (use the first character of each string)
•define, float, exp, char, atan, ceil, acos, floor.
There are several strings which have the same hash-key, it’s float and floor (hash-key:5), char and ceil (hash-key: 2). It’s called a collision. How can we handle this? there are 2 way:
•define, float, exp, char, atan, ceil, acos, floor.
There are several strings which have the same hash-key, it’s float and floor (hash-key:5), char and ceil (hash-key: 2). It’s called a collision. How can we handle this? there are 2 way:
1. Linear Probing
Search the next empty slot and put the string there.
Linear probing has a bad search complexity if there are many collisions.
example:
h[ ]
|
Value
|
Step
|
0
|
atan
|
1
|
1
|
acos
|
2
|
2
|
char
|
1
|
3
|
define
|
1
|
4
|
exp
|
1
|
5
|
float
|
1
|
6
|
ceil
|
5
|
7
|
floor
|
3
|
…
|
2. Chaining
In chaining, we store each string in a chain (linked list).
So if there is collision, we only need to iterate on that chain.
example:
h[ ]
|
Value
|
0
|
atan à acos
|
1
|
NULL
|
2
|
char à ceil
|
3
|
define
|
4
|
exp
|
5
|
float à floor
|
6
|
NULL
|
7
|
NULL
|
…
|
Blockchain
A blockchain is also a distributed data structure but its purpose is completely different.
Think of it as a history, or a ledger. The purpose is to store a continuously-growing list of record without the possibility of tampering and revision.
It is mainly used in the bitcoin currency system for keeping track of transactions. Its property of being tamper-proof let everybody know the exact balance of an account by knowing its history of transaction.
In a blockchain, each node of the network stores the full data. So it is absolutely not the same idea as the DHT in which data are divided among nodes. Every new entry in the blockchain must be validated by a process called mining whose details are out of the scope of this answer but this process insure consensus of the data.
The two structures are both distributed data structure but serve different purposes. DHT aims to provide an efficient (in term of lookup time and storage footprint) structure to divide data on a network and blockchain aims to provide a tamper-proof data structure.
Tree Concept
•Node at the top is called as root.
•A line connecting the parent to the child is edge.
•Nodes that do not have children are called leaf.
•Nodes that have the same parent are called sibling.
•Degree of node is the total sub tree of the node.
•Height/Depth is the maximum degree of nodes in a tree.
•If there is a line that connects p to q, then p is called the ancestor of q, and q is a descendant of p.
Binary Tree Concept
• Binary tree is a rooted tree data structure in which each node has at most two children.
• Those two children usually distinguished as left child and right child.
• Node which doesn’t have any child is called leaf.
• Binary search tree also can be used for converting infix to prefix and postfix conversion
• Types of binary tree:
1. PERFECT binary tree is a binary tree in which every level are at the same depth.
2. COMPLETE binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. A perfect binary tree is a complete binary tree.
3. SKEWED binary tree is a binary tree in which each node has at most one child.
4. BALANCED binary tree is a binary tree in which no leaf is much farther away from the root than any other leaf (different balancing scheme allows different definitions of “much farther”).
Threaded Binary Tree Concept
• In one way threading, a thread will appear either in the right field or the left field of the node.
• A one way threaded tree is also called a single threaded tree.
• If the thread appears in the left field, then the left field will be made to point to the in-order predecessor of the node.
• Such a one way threaded tree is called a left threaded binary tree.
• On the contrary, if the thread appears in the right field, then it will point to the in order successor of the node. Such a one way threaded tree is called a right threaded binary tree.
• Advantages:
1. It enables linear traversal of elements in the tree.
2. Linear traversal eliminates the use of stacks which in turn consume a lot of memory space and computer time.
3. It enables to find the parent of a given element without explicit use of parent pointers.
4. Since nodes contain pointers to in-order predecessor and successor, the threaded tree enables forward and backward traversal of the nodes as given by in-order fashion.
•Binary Search Tree (BST) is one such data structures that supports faster searching, rapid sorting, and easy insertion and deletion.
•BST is also known as sorted
versions of binary tree.
•For a node x in of a BST T,
–the left subtree of x contains elements that are smaller than those stored in x,
–the right subtree of x contains all elements that are greater than those stored in x, with the assumptions that the keys are distinct.
•Binary Search Tree has the following basic operations:
vfind(x) : find key x in the BST
vinsert(x) : insert new key x into BST
vremove(x) : remove key x from BST